Three Situations When Our Brain Works Against Us

Our brain is out to get us! When we have to make critical decisions under uncertainty, it uses inappropriate mental shortcuts instead of solid reasoning. And we are not even aware that this is happening.

Brain Fooling Us

Example.

A software vendor describes their product and points out several benefits that they think are especially relevant to you. They give examples of some companies who bought their product. They give you prices for various volumes or tiers. The decision you need to make: should you buy this?

Making the decision requires estimating several unknowns, in a series of steps:

How likely is your company to significantly benefit from the product? This would determine whether the product is worth investigating further.
How frequent are the various use cases for the product in your company? This would determine what use cases to investigate first—the most frequent ones (it’s too much effort to investigate all).
What is the likely benefit in dollar value? You estimate the likely benefit of the product for an instance of each use case you investigated.

You could stop at any of the steps. If you made it through, you compare the total estimated benefit to the known cost, and make a go or no-go decision.

Nicely done!

Oh wait… The above is a theoretical model. In reality, at every step of the process, you are estimating some unknowns, and if your estimates are wrong you will make the wrong decision: you will either overypay by buying the product, or miss an opportunity by not buying it.

Mental Shorcuts.

All the previous questions are about probability. There are two ways of dealing with probability: intuition, and methodical reasoning. When faced with a problem that requires methodical reasoning to solve, our brain fools us and uses intuition instead. Specifically, it replaces:

The harder problem of “how likely?” with the easier “how similar?”. Instead of anwering, “How likely is my company to belong to the set of companies that could benefit from the product?”, our brain asks, “How similar is my company to the stereotype of companies benefiting from the product?”. Unfortunately, your company might be quite different from the stereotype of the product’s users but still have a great need for the product.
The harder problem of “how frequent?” with the easier “how easy to recall?” Instead of answering, “How common are the use cases of the product?” our brain asks “How easily can I remember instances of these use cases?” Chances are, unless you are intimately familiar with the product’s use cases, you likely have encountered the use cases infrequently or not at all, and you don’t know the true frequency.
The harder problem of “how much?” with the easier “pick an arbitrary number that we can relate to; now adjust up/down—does it feel about right?”.

These mental shortcuts are evolutionarily adaptive mechanisms that helped our ancestors survive in a hostile world. They helped our ancestors make decisions quickly, when a slow decision was worse than a sub-optimal decision.

Imagine a pre-historic human foraging for fruits in a forst, and trying to methodically compute the probability that the rustling in the trees is a lion or something harmless. Yup, that human got eaten one day while he/she was still calculating.

Our ancestors were the ones who did not compute probabilities laboriously but instead used heuristics: I remember someone was eaten by a lion 2 days ago; that lion might be around—let’s run away.

In the modern world, few decisions require making life-and-death decisions in seconds or minutes. We can take the time to think things through, but our brain does not want to do that.

Decision Making Process Model

All models are wrong. Some are useful. —Everybody

The model below introduces the key aspects of the process of decision making that are relevant to this discussion.

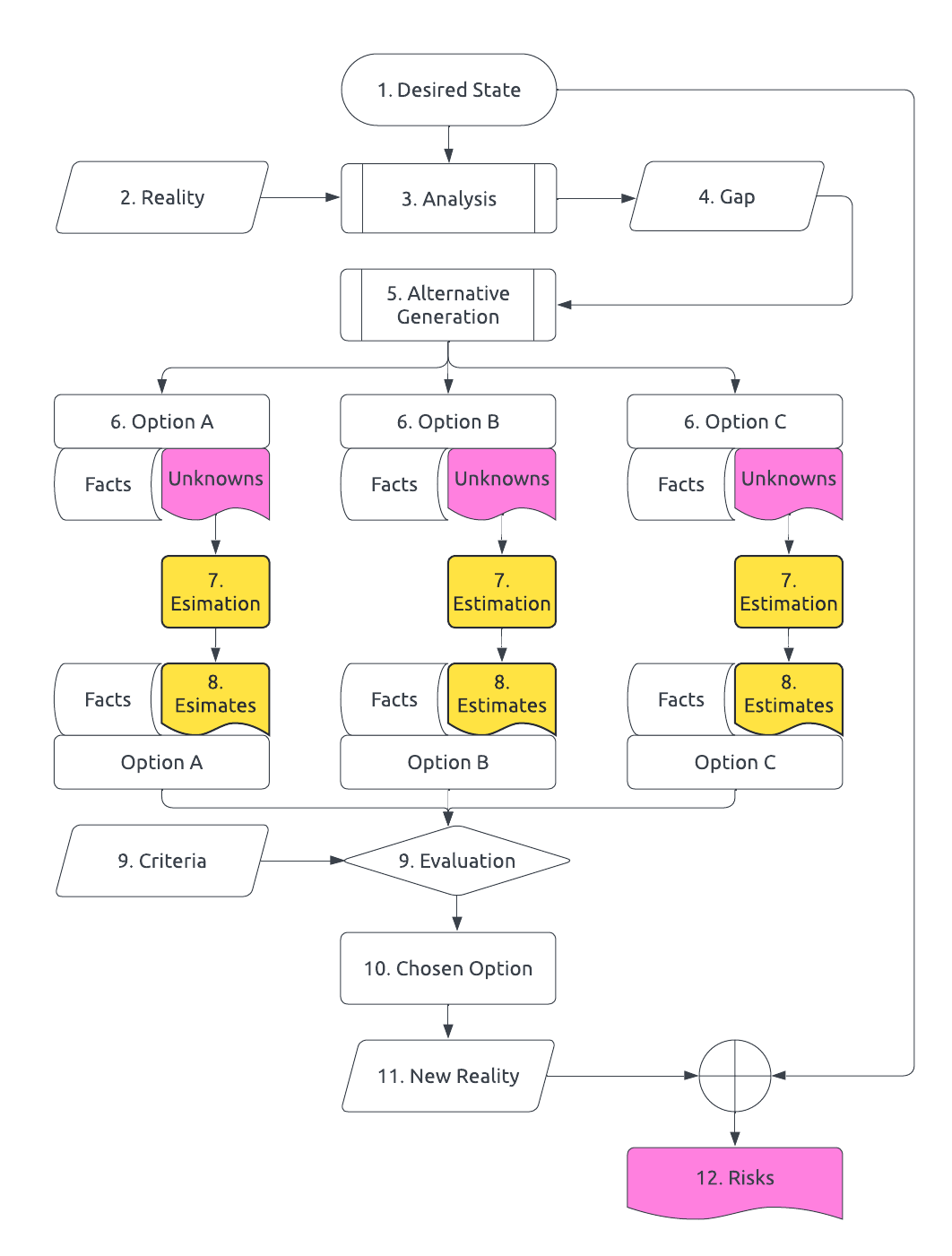
A Model of Decision Making

In this model, the process of decision making is:

We imagine a desired state.
We observe the current reality.
We do a lot of thinking.
We identify the gap.
We imagine ways we could reduce the gap.
We arrive at some options. For each option, there are attributes whose values we know (“facts”) and attributes whose values we don’t (“unknowns”).
For each unknown, we attempt to estimate it.
The resulting estimates replace the unknowns.
We use a decision algorithm to compute the desirability of each option using the values of its attributes. The algorithm usually is filter-and-rank, guided by some evaluation criteria.
We choose the top ranked option and implement it.
Our actions affect reality.
If we didn’t choose the best option, we are not as close to the desired state as we wanted. This is risk.

Risk can occur due to flaws at any step of the process. I want to focus on the steps that require estimation.

Defining Risk

Conceptually, there is an objective best option, but we don’t know which one it is because of unknowns.

If we had all the necessary facts with no unknowns, we would be able to deterministically compute the gain and cost of each option.

We usually can’t eliminate all the unknowns. The best we can do is to make an estimate for each unknown. This leads to an estimated gain and cost of each option.

If we make an incorrect estimate, our decision algorithm may pick the non-optimal option. Choosing the non-optimal option means we may incur more cost for less gain, compared to the optimal option. Let’s call the difference between the chosen option and the optional option the negative impact.

Let’s define risk of an option as: the probability of choosing that option, times the negative impact of choosing that option.

The overall risk is simply the sum of the risks of each option.

Estimation and Heuristics

Most estimation problems boil down to:

Likelihood. How likely is object α to belong to the class A?
Frequency. Does A occur more frequently than B?
Value. What is the likely value of α? (More precisely, what is the range of values α could have with probability p?)

Once the problem statement has been identified, a range of methods ranging from back-of-the-envelope to tools-and-number-crunching can be applied.

To get an idea of the available methods, see:

Selecting the right method requires that we define the estimation problem correctly. And therein lies a big problem: our brain does not let us see the estimation problem for what it really is.

System 1 and System 2

There is much research supporting the idea that our brains use two entirely different processes for solving problems, called System 1 and System 2.

System 1 is unconscious and automatic, fast, effortless, emotional, and relies on stereotypes. Our brain engages it for things like:

Localizing the direction of the source of a sound
Solving 2 + 2 = ...
Understanding simple sentences
Reacting emotionally to a picture

System 2 is conscious and deliberate, slow, effortful, emotionless, and relies on logic and computation. Our brain engages it for things like:

Determining the nature of the source of an unfamiliar sound
Solving 35 x 17 = ...
Determining the correctness of a complex logical argument
Finding an obscure or hidden object in a picture

The estimation problems mentioned earlier require System 2 thinking, which requires deliberate effort. Our brain subsitutes the problem with an easier one that requires a System 1 heuristic, without us being aware of this substitution.

Problem to be Solved	Heuristic
Likelihood. How likely is it that object `α` belongs to class `A`?	Representativeness. How similar is `α` to the stereotype of class `A`?
Frequency. Does `A` occur more frequently than `B`?	Availability. Can I remember more instances of `A` than `B`?
Value. What is the likely value of `α`?	Anchoring. Pick an (arbitrary) number and adjust it up or down until it feels right

Heuristic 1: Representativeness

When faced with the question “How likely is it that object α belongs to class A?”, our brain uses the heuristic “How similar is object α to the stereotype of class A (or not-A)?.” These are not the same questions. To see why, read the experimental evidence below.

Problems with this heuristic: (a) We think the limited information about similarity is more predictive than it really is; we neglect to think of other pertitent unknowns about similarity; (b) We ignore the “base-rate” of class A: how common is the class, to start with?

Representativeness: Experimental Evidence

Researchers conducted several experiments, asking subjects to estimate the probability that a given individual was an engineer or lawyer. They divided subjects into two groups for each experiment. Group 1 was told that the population consisted of 70 engineers and 30 lawyers. Group 2 was told that the population consisted of 30 engineers and 70 lawyers.

Experiment A: Predicting Class When No Other Information is Available.

The researchers gave subjects no additional information about the given individual.

Subjects in group 1 predicted there was a 70% chance the individual was an engineer, and those in group 2 predicted a 30% chance.

This is as expected: since subjects had no other information than the population ratio, they used it for their likelihood predictions. So far, so good.

Things become interesting when additional information is present.

Experiment B: Predicting Class When Some Predictive Information is Present.

The researchers constructed brief descriptions of a stereotypical engineer (“an introverted, analytical man”) and stereotypical lawyer (“an extroverted man who loves debates”). They randomly gave one or other description to subjects across the groups.

Subjects in both groups predicted that the individual was an engineer or lawyer with near 100% probability, in accordance to the description they were given. They completely ignored the population ratio they were given beforehand.

This is not logical.

While the description “an introverted, analytical man” does arguable match the stereotypical engineer, do all such individuals become engineers? Can at least a few lawyers be introverted and analytical? What about other (unstated) personanlity traits that could also affect choice of occupation? What about environmental factors like parent’s occupations or preferences? There are many reasons an introverted and analytical person might have become a lawyer instead of an engineer: just from the description itself, the probability is not 100%.

Experiment C: Predicting Class When Non-Predictive Informatoin is Present.

The researchers constructed detailed descriptions of the individual, which nevertheless had no predictive power: it could apply either to an engineer or lawyer equally well. E.g.: “Dick is a 30 year old man. He is married with no children. A man of high ability and motivation, he promises to be quite successful in his field. He is well liked by his colleagues.”

Subjects in both groups predicted that the individual is equally likely to be engineer or lawyer. They completely ignored the population ratio they were given beforehand.

Again, this is not logical.

The description did not provide any useful information about the occupation and subjects should have just ignored it. Instead, subjects relied almost entirely on the inconclusive description. Since the description was equally similar to a stereotypical engineer or lawyer, they incorrectly concluded that the individual was equally likely to be an engineer or lawyer.

Heuristic 2: Availability

When faced with the question “Is the frequency of class A greater than B?”, our brain uses the heuristic “Can I recall more examples of class A than class B?” These are not the same questions. To see why, read the experimental evidence below.

Problems with this heuristic: (a) Whether we can recall instances of class A has more to do with how our memory works (some things are easier to recall than others) than the real frequency of A; (b) we are over-confident that our own exposure to A is representative of its true prevalence.

Availability: Experimental Evidence

Experiment A: First Letter or Third Letter.

Researchers chose a small set of letters from the English alphabet which occur more often in the third place than in the first place of words in English.

They randomly assigned letters to subjects—all native English speakers—and asked: “do more words start with this letter, or do more more words contain this letter in the third position.” Almost everyone judged, incorrectly, that more words start with the letter they were given.

The effect can be explained by the observation that it is much easier to recall words that start with a given letter, than to recall words that contain some letter in the third place. What effectively happened was, the subjects asked themselves, “How many words can I recall starting with this letter? How many words with this letter in third place?” Since they could recall more words which started with the given letter, they predicted this class was more likely.

Experiment B: More Men or More Women.

Researchers divided subjects into multiple groups, and recited a list of well-known personalities to each group. Different groups were presented with different lists: in some lists the men were more famous than women, and in others the women were more famous. They then asked each group: were there more men than women in the list presented to them?

Each group incorrectly judged that the list presented had more names of the gender that had the more famous names. In reality, the lists contained an equal number of men and women.

This effect can be explained by the observation that it is easier to recall famous names compared to less famous or unknown names.

Experiment C: Probability of Traffic Accidents.

When people are asked to estimate the probability of traffic accidents, they rate the probability higher if they have recently observed an accident, and rate it lower if they haven’t observed an accident recently.

Heuristic 3: Anchoring

When faced with the question “What is the likely value of α?”, our brain uses the heuristic “Guess an arbitrary number; then, adjust it up or down until it feels right”. Sounds unbelievable? Not something you’d ever do? See the experimental evidence below.

Problems with this heuristic: (a) Our initial guess is “anchored” to—is influenced highly by—the last number we paid attention to, even if that is not related to the current situation; (b) We are over-confident about how close to the real value our initial guess is; because of this over-confidence, we do not spend the effort required to gain factual information; (c) We start feeling right too quickly, before making enough adjustment.

Anchoring: Experimental Evidence

Experiment A: Estimating Unfamiliar Quantities.

Researchers divided subjects into several groups. For each group, they spun a wheel-of-fortune and announced the resulting number. The researchers then posed an estimation question and asked the participants:

Do you think the number from the wheel-of-fortune is higher or lower than the quantity we just asked you to estimate?
Now, create an estimate for the question we just asked you.

For each group and each question, the arbitrary number from the wheel-of-furtune had a significant effect on the estimate.

E..g, one of the questions was: “What percentage of African countries are members of the United Nations?” Group 1 was given the number 10 from the wheel-of-furtune; their average estimate was that 25% of African countries are UN members. Group 2 was given the number 65 from the wheel-of-furtune; their average estiamte was that 45% of African countries are UN members.

Even though the subjects knew that a number from a wheel-of-fortune has nothing to do with the question posed, they were strongly influenced by it.

(Both groups were far off the mark: the real number is 90%.)

Experiment B: Estimating the Product of 8 numbers.

Researchers divided high-school students into two groups, gave them a multiplication problem and asked them to estimate the result in less than 5 seconds. The time limit ensured that no one would be able to actually do the computation, and be forced to estimate.

Group 1 was asked to estimate 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1; their median estimate was 2250. Group 2 was asked to estimate 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8; their median estimate was 512.

Note that the numbers are exactly the same but in different orders. Why the big difference in estimates?

This effect can be explained by the observations:

Under time pressure, people would perform the first 2-3 multiplications, and then guess a number than was ~3 times higher. Those who were given the numbers in descending order started with a larger number than those who were given the numbers in ascending order.
Group 1 would adjust their guess down to account for the descending order; Group 2 would adjust their guess up to account for the ascending order.
Almost always, we don’t adjust enough.

(The correct result for both questions is 40,320. Both groups were very far off.)

Postscript

Pop psychology. The internet and bookstores are full of content about how the human mind works and how we make decisions (or should make them). Much of this content is not fact based: it is opinion, speculation or pseudo-science. Most authors over-generalize from a limited set of anecdotes, and present this as universal truth, or cherry pick their facts and do not make an honest attempt at finding or presenting evidence that might contradict their opinion. The right way to deal with such content is to recognize and treat it as such: an opinion that might be applicable but is not guaranteed to.

The content that is bona-fide fact-based is sometimes outdated or proven to be incorrect, but persists in our minds. Examples are the Dunning-Kruger Effect, and the book Outliers: The Story of Success by Malcolm Gladwell. The authors reported what they found, extrapolated to some conclusion, and did not attempt to cheat anyone. Subsequently, the evidence they’ve relied on has been shown to have different, equally or more plausible explanations. However, their original conclusions were very compelling, and they get cited a lot; the caveats do not.

The damage of unjustified confidence in particular narratives is not just to the individuals claiming them, but to organizations and entire societies.

Evidence based research.

There is obervation- or experiment-based research about the human mind. But the specialized nature, technical jargon and sheer volume of evidence-based research about the human mind is not easily accessible to the layperson.

We need people who can summarize research for the layperson. They need to be able to keep track of research and interpret which pieces have been validated enough vs which are speculative, and then they need to choose the highlights and rewrite them in non-tecnical language. This is no small request!

The best people to do so would be academics who are actively researching and teaching in the field. Is there any incentive for them to take the effort of summarizing and translating tecnical research for lay-people? No.

You have never heard true condescension until you have heard academics pronounce the word ‘popularizer’ — James Boyle.

Fortunately, some practising scientists have made the effort to summarize vast amount of research conducted over decades into language that is accessible to us, without sacrificing accuracy. Some authors I trust are:

How the human mind works and develops:

How to reduce uncertainty:

Cognitive biases:

Daniel Kahneman